Patient Care under Uncertainty in Normal and COVID-19 Times
NBER Reporter 2020:2
Patient Care under Uncertainty in Normal and COVID-19 Times
Charles F. Manski

Charles F. Manski has been Board of Trustees Professor in Economics at Northwestern University since 1997. He previously was a faculty member at the University of Wisconsin-Madison (1983–98), the Hebrew University of Jerusalem (1979–83), and Carnegie Mellon University (1973–80). He received his BS and PhD in economics from MIT in 1970 and 1973. He has received honorary doctorates from the University of Rome Tor Vergata (2006) and the Hebrew University of Jerusalem (2018).
Manski's research spans econometrics, judgment and decision, and analysis of public policy. He is an author of numerous books including Patient Care under Uncertainty (2019), Public Policy in an Uncertain World (2013), Identification for Prediction and Decision (2007), Social Choice with Partial Knowledge of Treatment Response (2005), Partial Identification of Probability Distributions (2003), Identification Problems in the Social Sciences (1995), and Analog Estimation Methods in Econometrics (1988), and coauthor of College Choice in America (1983). He has served as director of the Institute for Research on Poverty (1988–91).
Manski is an elected Member of the National Academy of Sciences, an elected Fellow of the American Academy of Arts and Sciences, the Econometric Society, the American Statistical Association, and the American Association for the Advancement of Science, a Distinguished Fellow of the American Economic Association, and a Corresponding Fellow of the British Academy.
Over the past 10 years, I have increasingly focused my research on patient care under uncertainty. By uncertainty, I do not only mean that clinicians make probabilistic rather than deterministic predictions of patient outcomes. I mean that available knowledge may not suffice to yield precise probabilistic predictions. A patient may ask: "What is the chance that I will develop disease X in the next five years? What is the chance that treatment Y will cure me?" A credible response may be a range, say, 20 to 40 percent, or at least 50 percent. While most of my research appears in technical journals, in a recent book, Patient Care under Uncertainty, I present a largely verbal summary to make the findings accessible to a broader audience.1
Choice under Uncertainty and Econometrics
I often consider the choice between surveillance and aggressive treatment.2 For patients with treated localized cancer who are at risk of metastasis, surveillance may mean scans, and aggressive treatment may be chemotherapy or immunotherapy. For patients with COVID-19, surveillance may mean self-care at home, and aggressive treatment may mean hospitalization. Aggressive treatment may reduce the risk of disease development or the severity of disease that does develop. However, it may generate health side effects and financial costs beyond those associated with surveillance.
I have had no formal training in medicine. The contributions that I feel able to make concern the methodology of empirical medical research, also called evidence-based medicine. This lies within the expertise of econometricians, statisticians, and decision analysts. For example, in recent work with Anat Tambur and Michael Gmeiner, I have developed new methods for predicting the graft-survival outcomes of patients who receive kidney transplants, given observation of organ quality, patient age, and the degree of genetic match between donor and patient.3
Research on medical treatment response and risk assessment shares a common objective: probabilistic prediction of patient outcomes conditional on observable patient attributes. Development of methodology for probabilistic conditional prediction has long been a core concern of econometrics. Prediction methods may be called regression, actuarial prediction, statistical prediction, machine learning, predictive analytics, or artificial intelligence.
Statistical imprecision and identification problems limit the predictive power of empirical research. Statistical theory characterizes the inferences that can be drawn about a study population by observing a sample. Identification analysis studies inferential problems that persist when sample size grows without bound. My research has focused mainly on identification, which often is the dominant difficulty.4
A fundamental identification problem in the analysis of treatment response is the unobservability of counterfactual treatment outcomes. Another important problem is characterization of external validity, that is, the feasibility of extrapolation from study populations to patient care. There are also many common problems of imperfect data quality, including measurement errors and missing data.
Credible research may be able to bound the probability that an event will occur, but not to make precise probabilistic predictions, even with large data samples. This situation is known as partial rather than point identification. Study of partial identification differs from the traditional focus of econometrics on point estimation. The latter requires strong assumptions. Partial identification, instead, begins by posing weak assumptions that should be credible in the applied context under study. Weak assumptions commonly yield estimates of ranges, "set estimates," rather than point estimates. Studies of partial identification aim to determine the set estimates that result when available data are combined with specified assumptions.
I am concerned with the implications of identification problems for decision-making. How might one choose between treatment A and treatment B when one cannot credibly identify the sign, let alone the magnitude, of the average treatment effect of A versus B? There is no optimal way to choose, but I suggest that there are reasonable ways. For example, in recent work with Rachel Cassidy, I have combined partial identification analysis with decision theory to study diagnosis and treatment of tuberculosis when existing diagnostic tests have uncertain accuracy.5 Our methodology should also be applicable to diagnosis and treatment of COVID-19.
Some of my work has been critical of methodologies that are used widely in medical research. I have warned against use of the statistical theory of hypothesis testing to design and analyze randomized trials, instead recommending the application of statistical decision theory.6,7 While the common view is that empirical research on treatment response should solely or predominantly use evidence from randomized trials, I have argued that both trial findings and observational data are partially informative when interpreted with credible assumptions.8,9
My research bears on treatment choices that arise in the context of the coronavirus pandemic. Because of its current relevance, and because it illustrates my research strategy, I therefore focus the remainder of this summary on this new work.
Estimating the COVID-19 Infection Rate
Accurate characterization of the time path of the coronavirus pandemic has been hampered by a serious problem of missing data. Confirmed cases have been measured by rates of positive findings among persons who have been tested for infection. Infection data are missing for persons who have not been tested. The persons who have been tested differ from those who have not been tested. Criteria used to determine who is eligible for testing typically require demonstration of symptoms associated with the presence of infection or close contact with infected persons. This gives reason to believe that some fraction of untested persons are asymptomatic or pre-symptomatic carriers of the COVID-19 disease.
In addition, the measurement of confirmed cases is imperfect because the prevalent nasal swab tests for infection are not fully accurate. Combining the problems of missing data and imperfect test accuracy yields the conclusion that reported cumulative rates of infection are lower than actual rates. Reported rates of infection have been used as the denominator for computation of rates of severe disease conditional on infection, measured by rates of hospitalization, treatment in intensive care units, and death. Presuming that the numerators in rates of severe illness conditional on infection have been measured accurately, reported rates of severe illness conditional on infection are higher than actual rates.
Various research teams have put forward point estimates and forecasts for infection rates and rates of severe illness. These are derived in various ways and differ in the assumptions they use to yield specific values. The assumptions vary substantially and so do the reported findings. No assumption or estimate has been thought to be sufficiently credible to achieve consensus across researchers. Rather than reporting point estimates obtained under strong assumptions that are not well-justified, I find it more informative to determine the range of infection rates and rates of severe illness implied by a credible spectrum of assumptions.
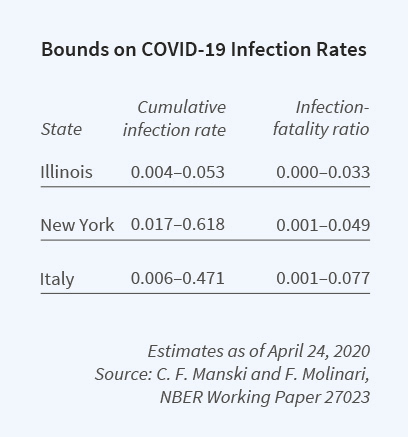
To this end, Francesca Molinari and I have brought to bear econometric research on partial identification.10 We explain the logic of the identification problem, determine the identifying power of some credible assumptions, and then combine available data with these assumptions to bound the cumulative infection rate for the coronavirus.
We focus on the cumulative infection rate from the beginning of the pandemic until specified dates. Our most important assumption is that the rate of infection among untested persons is lower than the rate among tested persons. Using this and other assumptions, we bound the population infection rate in Illinois, New York, and Italy over the period March 16 to April 24, 2020.
Bounding the Predictive Values of Antibody Tests
COVID-19 antibody tests have imperfect accuracy. Unfortunately, there has been a lack of clarity on the meaning of reported measures of accuracy. For risk assessment and clinical decision-making, the rates of interest are the positive and negative predictive values of a test. Positive predictive value (PPV) is the chance that a person who tests positive has been infected. Negative predictive value (NPV) is the chance that someone who tests negative has not been infected.
The medical literature regularly reports two key statistics: sensitivity and specificity. Sensitivity is the chance that an infected person receives a positive test result. Specificity is the chance that a non-infected person receives a negative result. Knowledge of sensitivity and specificity permits one to predict the test result given a person's true infection status. These predictions are not directly relevant to risk assessment or clinical decisions, where one knows a test result and wants to predict whether a person has been infected. Given estimates of sensitivity and specificity, PPV and NPV can be derived if one knows the prevalence of the disease, the overall rate of illness in the population. However, there is considerable uncertainty about the prevalence of COVID-19.
I have recently studied the problem of inference on the PPV and NPV of COVID-19 antibody tests given estimates of sensitivity and specificity and credible bounds on prevalence.11 I explain the methodological problem and show how to estimate bounds on PPV and NPV. I then apply the findings to some tests authorized by the US Food and Drug Administration, using the estimated bounds reported above on the infection rate in New York State. I find narrow bounds for NPV and wide bounds for PPV, given the current limited knowledge of prevalence. The table gives illustrative findings for one test.

COVID-19 Policy Assessment
My analysis of the epidemiological modeling used to predict the time path of the pandemic under alternative policies has emphasized two points12. First, integrated assessment of COVID-19 policy should consider the full health, economic, and social impacts of alternative policy options. Most epidemiological models, however, only consider the direct impacts on the health-care system. Since its inception a century ago, epidemiology has mainly been a subject studied by quantitative researchers with backgrounds in medicine and public health. Researchers with these backgrounds have found it natural to focus on health concerns. They tend to view the economy and social welfare as matters that may be important but that are beyond their purview.
Second, even within the traditional focus of epidemiology on disease dynamics, there is limited basis to assess the accuracy of the models that have been developed and studied. In this setting, forthright communication of uncertainty in the findings of research that aims to inform public policy is important.13 In a study of the problem of formulating vaccination policy against infectious diseases, I noted the general absence of communication of uncertainty in epidemiological modeling. 14
The underlying problem is the dearth of empirical evidence to specify realistic epidemiological models and estimate their parameters. In our modern interconnected society, epidemiologists have been largely unable to learn from randomized trials. Modeling has necessarily relied on observational data. Attempting to use the limited available evidence, epidemiologists have developed models that are sophisticated from mathematical and computational perspectives, but whose realism is unclear. Authors have typically provided little information that would enable assessment of the accuracy of the assumptions they make about individual behavior, social interactions, and disease transmission.
Looking ahead toward integrated assessment of COVID-19 policy, I see lessons to be learned from research on climate policy. Climate research was at first a subject for study by earth scientists. With backgrounds in the physical sciences, these researchers find it natural to focus on the physics of climate change rather than on behavioral responses and social impacts. Over the past 30 years, the study of climate policy has broadened with the development of integrated assessment models, with major contributions by economists. As a result, we now have a reasonably sophisticated qualitative perspective on how our planet and our social systems interact with one another, albeit with a less than adequate ability to make credible quantitative predictions. My hope is that epidemiologists will emulate the efforts of climate researchers to develop integrated assessment models and to improve the credibility of their quantitative modeling.
1.
Patient Care under Uncertainty, Manski C. Princeton, NJ: Princeton University Press, 2019.
↩
2.
"Credible Ecological Inference for Personalized Medicine: Formalizing Clinical Judgment," Manski C. NBER Working Paper 22643, September 2016, and published as "Credible Ecological Inference for Medical Decisions with Personalized Risk Assessment," Quantitative Economics 9(2), July 2018, pp. 541–569.
↩
3.
"Predicting Kidney Transplant Outcomes with Partial Knowledge of HLA Mismatch," Manski C, Tambur A, Gmeiner M. Proceedings of the National Academy of Sciences 116(41), October 2019, pp. 20339–20345.
↩
4.
Identification for Prediction and Decision, Manski C. Cambridge, MA: Harvard University Press, 2007.
↩
5.
"Tuberculosis Diagnosis and Treatment under Uncertainty," Cassidy R, Manski C. Proceedings of the National Academy of Sciences 116(46), November 2019, pp. 22990–22997.
↩
6.
"Statistical Treatment Rules for Heterogeneous Populations: With Application to Randomized Experiments," Manski C. NBER Technical Working Paper 242, May 1999, and published as "Statistical Treatment Rules for Heterogeneous Populations," Econometrica 72(4), July 2004, pp. 1221–1246.
↩
7.
"Statistical Decision Properties of Imprecise Trials Assessing COVID-19 Drugs," Manski C, Tetenov A. NBER Working Paper 27293, June 2020.
↩
8.
"Improving Clinical Guidelines and Decisions under Uncertainty," Manski C. NBER Working Paper 23915, October 2017, and published as "Reasonable Patient Care under Uncertainty," Health Economics 27(10), October 2018, pp. 1397–1421.
↩
9.
"Meta-Analysis for Medical Decisions," Manski C. NBER Working Paper 25504, January 2019, and published as "Toward Credible Patient-Centered Meta-Analysis," Epidemiology 31(3), May 2020, pp. 345–352.
↩
10. "Estimating the COVID-19 Infection Rate: Anatomy of an Inference Problem," Manski C, Molinari F. NBER Working Paper 27023, April 2020, and Journal of Econometrics https://doi.org/10.1016/j.jeconom.2020.04.041
↩
11.
"Bounding the Predictive Values of COVID-19 Antibody Tests," Manski C. NBER Working Paper 27226, May 2020.
↩
12.
"COVID-19 Policy Must Take All Impacts into Account," Manski C. Scientific American, March 28, 2020.
↩
13. "Communicating Uncertainty in Policy Analysis," Manski C. Proceedings of the National Academy of Sciences 116(16), April 2019, pp. 7634-7641.
↩
14.
"Vaccine Approvals and Mandates Under Uncertainty: Some Simple Analytics," Manski C. NBER Working Paper 20432, August 2014, and published as "Mandating Vaccination with Unknown Indirect Effects," Journal of Public Economic Theory 19(3), June 2017, pp. 603-619.
↩